Examples Relating to Three Variable Linear Equations 2X Y=6 3X Y= 4 X2Y 3Z=9X3YZ=6 X2Y3Z=7 2X3Y5Z=96X8YZ=22 Using the Elimination Method to Solve a Three Variable Linear Equation A threevariable linear equation is a bit more difficult to solve compared to equations with two variables This complexity is a result ofFree system of equations calculator solve system of equations stepbystep This website uses cookies to ensure you get the best experience By using thisQuiz 3 Linear Equations and Inequalities Click on the graphic to choose the correct graph The line through (3, 4) and (2, 3) Copy and paste this link in your browser The image should come up Click on the graphic to choose the correct graph Copy and paste this link in your browser

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 5
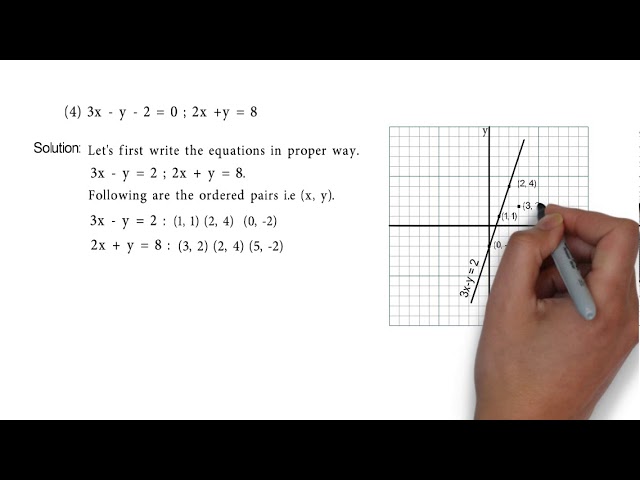
3x-y=2 2x-y=3 linear equation
3x-y=2 2x-y=3 linear equation-LAUGH Okay So let me, let's, let's make up a problem Let's say I had X plus 2x plus 3 is equal to, minus 7x minus 5 Well, in all of these linear equations, the first things that we, the first thing that we try to do is, get all of our variables on one side of the equation, and then get all of our concept terms on the other side of the Solve these simultaneous linear equations using elimination method 3a = 2b 1 and 3b = 5a 3 Mathematics X2y2=34,xy=2 solve for simultaneous quadratic equation math solve the simultaneous equation, giving your answer in base 2 11x11y=1001 10x y =10




無料ダウンロード 3x 2y5 X5 Y
Linear equation given in the question is, 2 3x 5 2x = y To simplify this equation further, Add like terms of the equation, (2 5) (3x 2x) = y 7 x = y Now compare this linear equation with the slopeintercept form of the linear equation, y = mx b Here, m = slope of the line' b = yintercept By comparing the equations,Algebra Graph y=2/3x2 y = − 2 3 x 2 y = 2 3 x 2 Rewrite in slopeintercept form Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Write in y = m x b y = m x b form Tap for more steps2x = y 3 and determine whether this system of linear equations has a unique solution or not Solution Since both the lines coincide Therefore infinitely many solutions
The system of linear equations x y z = 2, 2x y – z = 3, 3x The system of linear equations x y z = 2, 2x y – z = 3, 3x 2y kz = 4 has a unique solution if A k ≠ 0 B 1 < k < 1 C 2 < k < 2 D k = 0 Please scroll down to see the correct answer and solution guide 1 Answer 1 vote Write the equation in slopeintercept form y = mx b, where m is slope and b is y intercept y = 2x /3 3 Compare the equation with slopeintercept form y = mx b slope = 2/3 and y intercept is 3 y intercept is 3, so the line crosses the y axis at (0,3) Using slope find the next point Slope = rise/run = 2/3 Transcript Ex 32, 6 Given the linear equation 2x 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is (i) intersecting lines (ii) parallel lines (iii) coincident lines Given equation 2x 3y − 8 = 0 Therefore, a1 = 2 , b1 = 3 , c1 = –8 (i) For Intersecting
The simultanous equation calculator helps you find the value of unknown varriables of a system of linear, quadratic, or nonlinear equations for 2, 3,4 or 5 unknowns A system of 3 linear equations with 3 unknowns x,y,z is a classic example This solve linear equation solver 3 unknowns helps you solve such systems systematically Q5 Assertion The value of k for which the system of equations 3xky=0 and 2xy=0 has 2 ≠ b 1 /b 2 Answer Answer (a)Choose one of the equations and solve it for x by isolating x on the left hand side of the equal sign 3x=y2 Add y to both sides of the equation x=\frac {1} {3}\left (y2\right) Divide both sides by 3 x=\frac {1} {3}y\frac {2} {3} Multiply \frac {1} {3} times




Solve The Linear Equation Using Substitution Method 3x Y 2 2x Y 8 Maths Linear Equations In Two Variables Meritnation Com




4 3 Systems Of Linear Equations In Three Variables
Which of the following equations is not linear equation 2/3x 5 = 3x 4 2x 3 = 7x – 9 x 2 3 = 5x – 3 (x – 2) 2 = x 2 – 1 8 If x = 1,y = 1 is a solution of equation 9ax 12ay = 63 then, the value of a is 33 10 3/4 9 A linear equation in two variables has maximum Infinite solution Only one solution Two solution None ofY ′ = (x 3 − 3 x y 2 2) / (3 x 2 y − y 2) As the degree of numerator is greater than denominator we can simplify expression by dividing it to get y ′ = x Rearrange the equation to y = 2/3x 1, calculate two points on the line, eg (0,1) and (3,3), then draw the line passing through those two points You could try and find matching xs and ys by trial and error, but it is much more convenient to rearrange the equation so that one variable, say y, is isolated on the left side This way, we can pick any value for x we like and



1




Does The Pair Of Linear Equation Have No Solution Justify Your Ans 3x Y 3 0 2x 2 3y 2 No Spam Brainly In
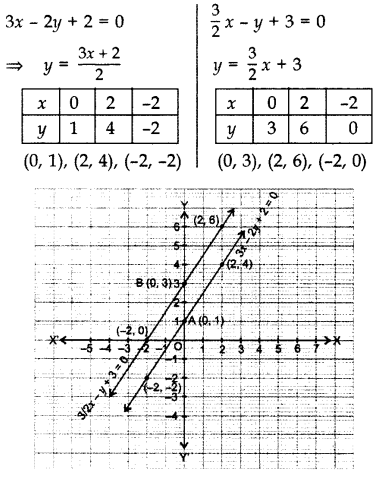
So let's divide everything by 2, and we get y is equal to 3x minus 2 So that's the second equation in slopeintercept form So same drill here The yintercept is negative 2 So we go that's negative 1, negative 2 right there, and its slope is 3 And notice its slope is the same as the other line So it's going to have the same inclination The equation 3x – 2y 2 = 0 meets the Yaxis at A(0,1) The equation \(\frac{3}{2}\)x – y 3 = 0 meets the Yaxis at B(0, 3) Question 7 Draw the graph of 2y = 4x – 6;The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Reorder 2 2 and 3 x 3 x y = 3 x 2 y = 3 x 2 y = 3x 2 y = 3 x 2 Use the slopeintercept form to find the slope and yintercept




Engineering Mathematics Notes




Linear Equations Algebra
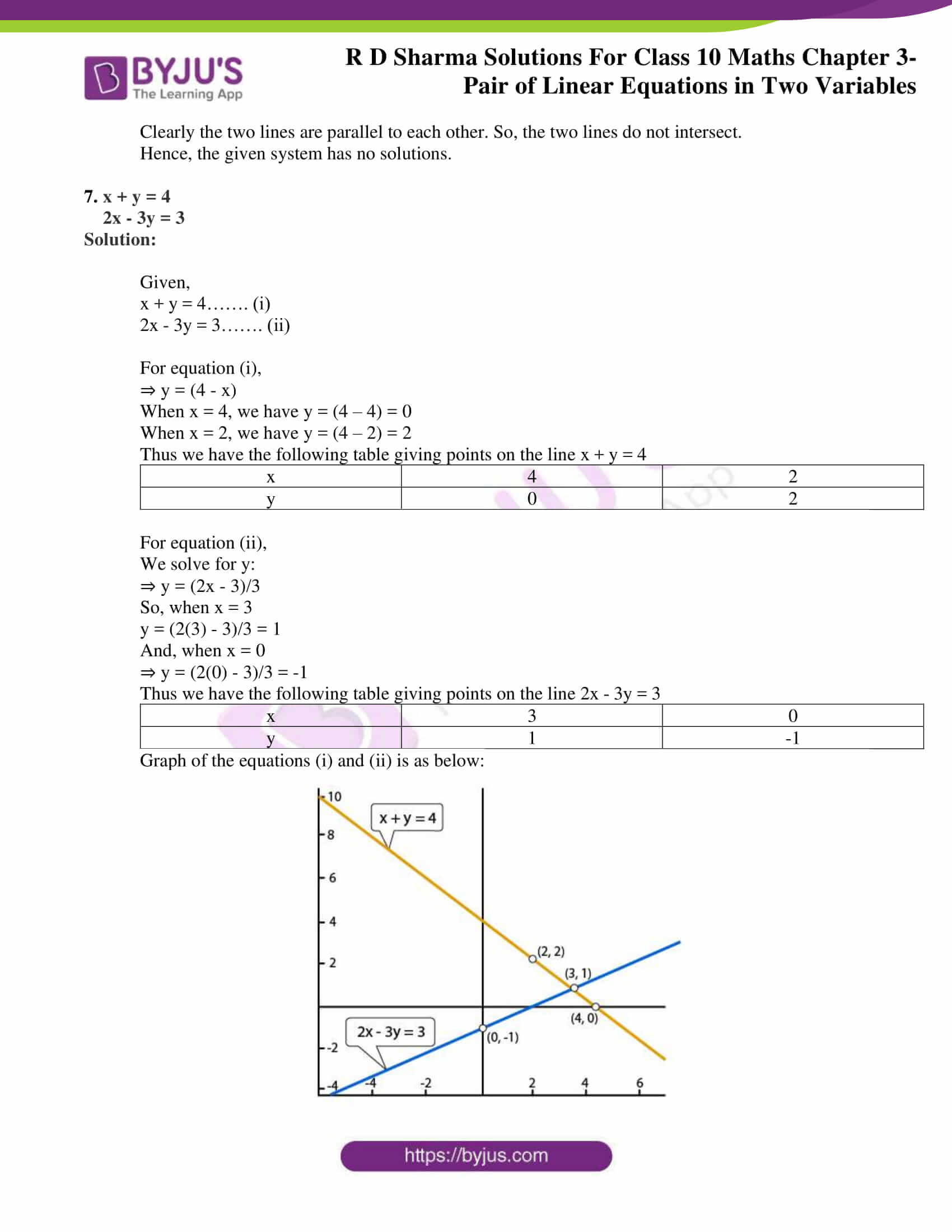
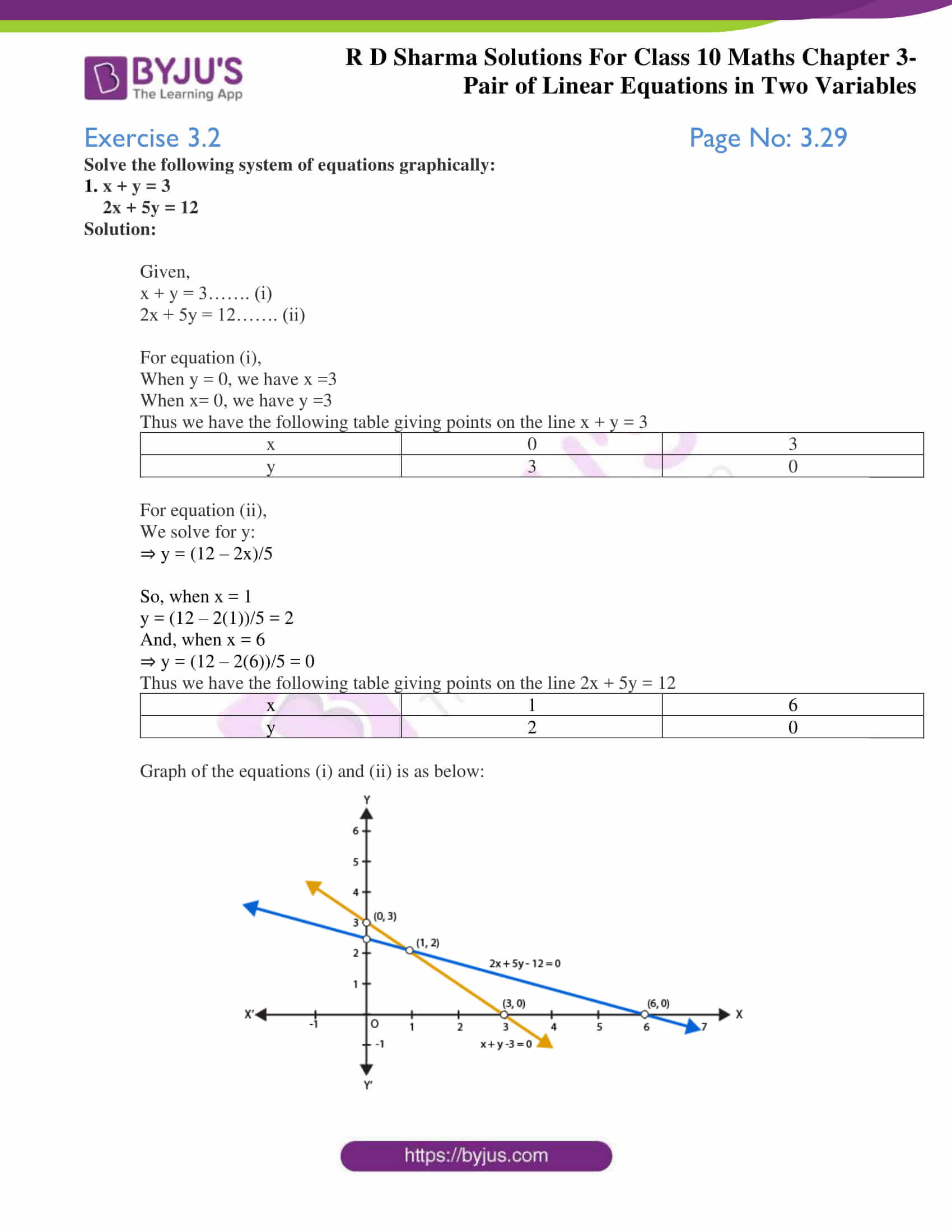
Find a few (x,y) pairs that satisfy the equation;Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank youChapter 3 Pair of Linear Equations in Two Variables Exercise – 32 Question 1 Solve the following of equation graphically x y = 3 2x 5y = 12 Solution 2x 5y = 12 We have, x y = 3 When y = 0 we have x = 3 When x = 0 we have y = 3 Thus we have the following table giving points on




Example If Lines 2x Y 3 0 5x Ky 3 0 Concurrent




無料ダウンロード 3x 2y5 X5 Y
Find the equation of the plane passing through the intersection of the planes 2x 5y – 5z = 6 and 2x 7y – 8z = 7 and the point (–1, 4, 3) asked in Threedimensional geometry by KumariMuskan ( 339k points)About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators y = 2x 4 2x y = 6 Solve the system of equations using substitution A) (2,8) B) (2,8) C) (10,24) D) no solution Algebra Create a system of equations that includes one linear equation and one quadratic equation Part 1 Show all work to solving your system of equations algebraically Part 2




If 2x Y 2 5 3x Y 1 3 2 X 2y 1 6 Then



Solve The Following Simultaneous Equations Graphically I 3x Y 2 0 2x Y 8 Ii 3x Y 10 X Y 2 Sarthaks Econnect Largest Online Education Community
Free linear equation calculator solve linear equations stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyClick here👆to get an answer to your question ️ The system of linear equations x y z = 2, 2x y z = 3, 3x 2y kz = 4 has a unique solution ifSince, the graph of linear equation 2x 3y = 6 cuts the yaxis, Put x = 0 in the given equation 2x 3y = 6 we get 2 × 0 3 y = 6 ⇒ 3 y = 6 ⇒ y = 6 3 ∴ y = 2 Hence, at the point (0, 2) the given linear equation cuts the yaxis



Solve The Following Simultaneous Equations Graphically I 3x Y 2 2x Y 3 Ii 3x 4y 7 5x 2y 0 Iii 2x 3y 4 3y X 4 Sarthaks Econnect Largest Online Education Community



3x Y 2 0 And 2x Y 8 Problem Set 1 Q3 4 Of Linear Equations In Two Variables Algebra Youtube
Solve the Following Simultaneous Equations Graphically3x – Y = 2 ;SOLUTION Directions Solve the system of equations by graphing {y=3x2 {y=2x3 Question Directions Solve the system of equations by graphing You can put this solution on YOUR website! On comparing the ratios of the coefficients of the following pairs of linear equations, we see that (i) x y = 5, 2x 2y = 10 have infinitely many solutions Hence, they are consistent (ii) x y = 8, 3x 3y =16 are parallel and have no solutionHence, the pair of equations are inconsistent




Solve The System Of Equations 2x 3y 17 3x 2y 6 By The Meth Scholr




Solve Graphically The Pair Of Linear Equation 3x Y 3 0 2x Y 8 0 Write The Coordinates Of The Vertices Of The Triangle Formed Maths Pair Of Linear Equations In Two Variables Meritnation Com
So, the graph of the equations x – y 1 = 0 and 3x 2y – 12 = 0 From the graph we conclude that the two lines intersect at A(2, 3) Also, we observe that the lines meet xaxis B(1, 0) and C(4, 0) So, x = 2 and y = 3 is the solution of the given system of equationsWhen x = 3, we have y = 3 2(3) = 3 6 = 3In order to graph these equations, we need to solve for y for each equation




Solve 2xy X Y 3 2 Xy 2x Y 3 10



Solve The Following Systems Of Equations Graphically 3x Y 1 0 2x 3y 8 0 Sarthaks Econnect Largest Online Education Community
Solve System of Linear Equations, Using Matrix Method 2x – Y = –2 3x 4y = 3 CBSE CBSE (Science) Class 12 Question Papers 1851 Textbook Solutions 2x – y = –2 3x 4y = 3 Advertisement Remove all ads Solution Show Solution The given system of equations can be written in the form of AX = B, where A linear equation can have more than one variable If the linear equation has two variables, then it is called linear equations in two variables and so on Some of the examples of linear equations are 2x – 3 = 0, 2y = 8, m 1 = 0, x/2 = 3, x y = 2, 3x – y z = 3 The graph of the line represented by the given equation is as shown iv) 3 = 2x y Rewrite the equations y = 3 2x Equation (1) By substituting the different values of x in Equation (1) we get different values for y When x = 0, we have y = 3 2(0) = 3 0 = 3;




Solved Stivity 2 Find My Valuel Solve The Following Given Problem X 6y 4 0 Y 3 2 4y 3x 3 Y 5x 5 X 3y 5 2x Y 5 3x 2y 17 2x 5y 14 3x




3x Y 2 0 2x Y 3 0 And A X 2ay 6 0 Are Concurrent Then Value Of A If The Lines 3x Y 2 Can Be B 7 14 A 7 1 X Drany Real Value C 1 7 X
Equation 1 y = 2x 1 Equation 2 y2 = 3x 1 Equation 3 y = 5x5 − 1 Equation 4 y = 4x4 − 1 Group of answer questions Equation 1 Equation 2 Equation3 Equation42x – Y = 3 Maharashtra State Board SSC (English Medium) 10th Standard Board Exam Question Papers 238 Textbook Solutions Graphical Method of Solution of a PairClick here👆to get an answer to your question ️ Do the following pair of linear equation have no solutionjustify your answer 3x y 3 = 0 and 2x 2/3y = 2




Ex 6 3 11 Solve 2x Y 4 X Y 3 2x 3y 6




無料ダウンロード 3x 2y5 X5 Y
Help a stranger please This is for my homework and I'm having a hard time solving these equations Show the complete solutions and final answers please It will be a great help Thank you so much This covers Additional Topics on Equations of Order One, Coefficient Linear in Two Variables 1 (6x3y2)dx(2xy1)dy=0 2 (x2y1)dx(2xy5)dy=0Divide \frac {2} {3}, the coefficient of the x term, by 2 to get \frac {1} {3} Then add the square of \frac {1} {3} to both sides of the equation This step makes the left hand side of the equation a perfect square x^ {2}\frac {2} {3}x\frac {1} {9}=\frac {y2} {3}\frac {1} {9} It is a line Liner equations have no X2 An example of a linear equation is x2 A linear equation also equals y=mxb It has a slope and a yintercept A nonlinear equation is also an equation in math It can have and x2 and it is not a line An example is y=x23x4 Non linear equations can be quadratics, absolute value or expodentail equations




6 Sol Or Solve The Following Pair Of Linear Equations Grap Scholr



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
2 y1(x) y2(x) y0 1(x) y0 2(x) = y1(x)y0(x)−y2(x)y0 1(x) THEOREM 3 Let y = y1(x) and y = y2(x) be solutions of equation (1), and let W(x) be their Wronskian Exactly one of the following holds (i) W(x) = 0 for all x ∈ I and y1 is a constant multiple of y2 (ii) W(x) 6= 0 for all x ∈ I and y = C1y1(x)C2y2(x) is the general solution ofConnect them Pick some values for x, and use the equation to find what y must be for each of those x's For example, if x is 0, then we have " "2xy=3 =>2(0)y=3 =>" "0y=3 =>" "y=3 So when x=0, we have y=3 Meaning the point (x,y)=(0,3) is a solution to 2xy=3, and so our graph of the equation will passA Step 1 B Step 2 C Step 3 D Step 4



How Do You Solve The System 2x Y 0 And 3x Y 10 By Graphing Socratic
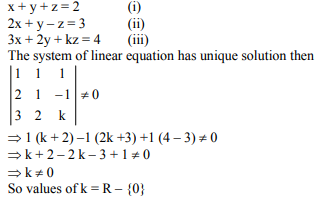



The System Of Linear Equations X Y Z 2 2x Y Z 3 3x 2y Kz 4 Has A Unique Solution Ifa K 0b For
A definition that I have used for a linear equation is A linear equation in one variable, x is an equation that can be written in the form ax b = 0, where a and b are real numbers, and a is not zero In our case, multiply both sides of the equation by 3 This yields 3 (2x/3 (x3) ) = 3 (4x) Ex 33, 1 (vi) Chapter 3 Class 10 Pair of Linear Equations in Two Variables (Term 1) Ex 33, 1 Solve the following pair of linear equations by the substitution method (vi) 3𝑥/2−5𝑦/3=−2 𝑥/3𝑦/2=13/6 Removing fractions from both equations 𝟑𝒙/𝟐−𝟓𝒚/𝟑=−2 Multiplying both equations by 6Quiz 3 Linear Equations and Inequalities Click on the graphic to choose the correct graph The line through (3, 4) and (2, 3) Copy and paste this link in your browser The image should come up Click on the graphic to choose the correct graph Copy and paste this link in your browser



How To Solve The Differential Equation 2x Y Dx 4x Y 6 Dy 0 Quora




Icise 111 Solve The Following Equations Graphically 1 X 3y 6 2x 3y 12 2 2x Y 6 2x Y 2 0 3 X
2 Look at the steps used when solving 3(x 2) = 3 for X 3(x 2) = 3 3x 6 = 3 3x 6 6 = 3 6 3x = 9 Write the original equation Use the Dist ributive Property Step 1 Step 2 3x 9 3 3 Step 3 x= 3 Step 4 Which step is the result of combining like terms?3x y = 2 2x y = 3 This pair of equations is "nicely" arranged for solving by variable elimination because one of the terms in the top equation that term is y is equal but with the opposite sign to the corresponding term in the bottom equation that term is y If you add these two equations vertically, the ycolumn will disappear because y added to y cancels out




Year 1 Quiz Systems Of Equations




Solve The Following Pair Of Linear Equations By Substitution Method 2x 3y 19 And 3x 2y 21




Standard Form Examples 3x Y 5 2x Y 10 X Y 6 Ppt Download



Draw The Graph Of Each Of The Following Linear Equations Class 9 Maths Cbse



1 Consistentdependentinconsistent One Solution Lines Intersect No Solution Lines Are Parallel Infinite Number Of Solutions Coincide Same Line Ppt Download




Example 28 Solve By Matrix Method 3x 2y 3z 8 2x Y Z 1 Examples



Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline




Solved In Exercises 11 22 Solve The System Of Linear Chegg Com



Systems Of Linear Equations




Linear Equations Algebra



Solving Linear Systems By Substitution Lesson 3 2




Solve 2xy X Y 3 2 Xy 2x Y 3 10 Mathematics Topperlearning Com X2oivz99
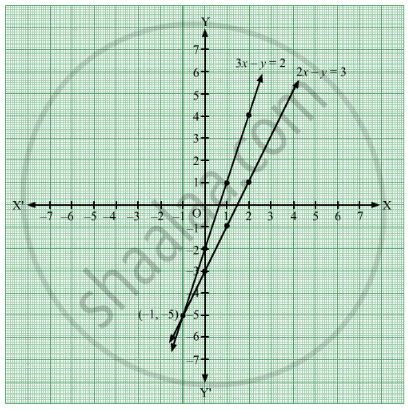



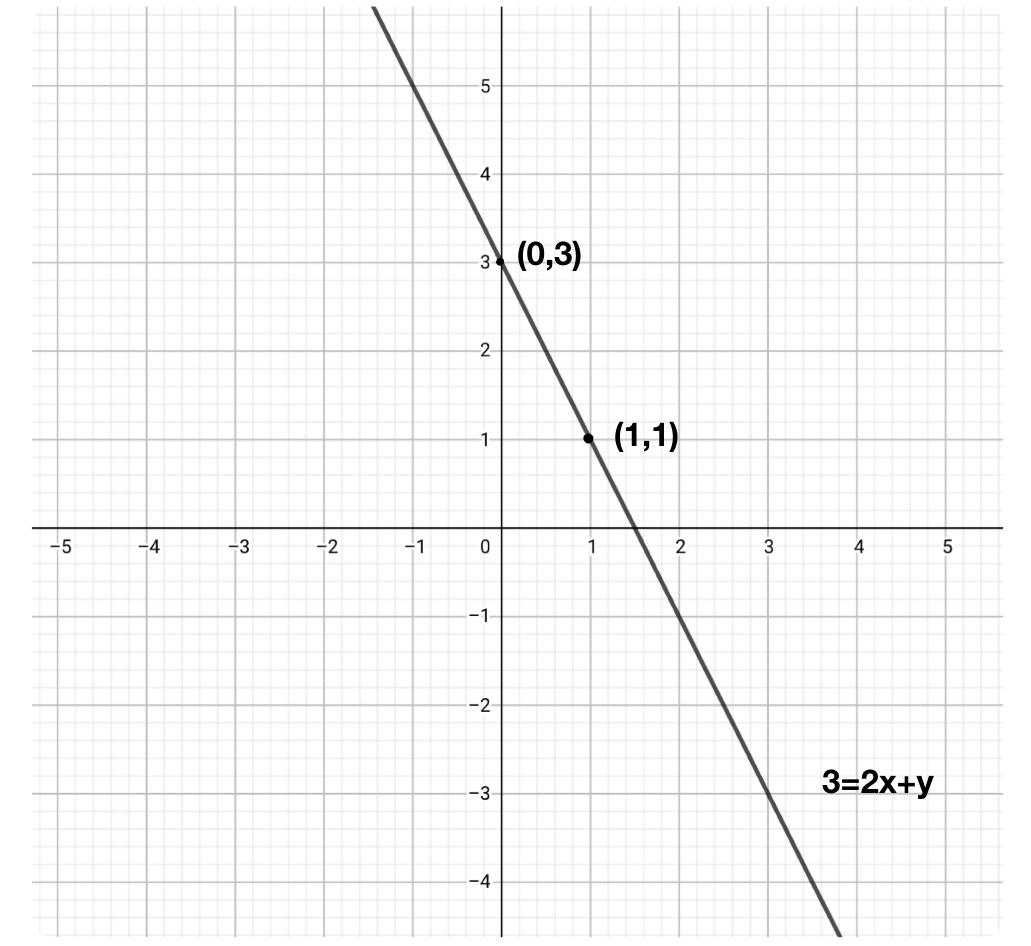
Solve The Following Simultaneous Equations Graphically 3x Y 2 2x Y 3 Algebra Shaalaa Com




Solve The System Of Equations 3x 3y 2z 1 X 2y 4 10y 3z 2 And 2x 3y Z 5 Answer Mathematics 1 Question Answer Collection



Do The Following Pair Of Linear Equations Have No Solution Justify Your Answer




Graph Graph Inequalities With Step By Step Math Problem Solver



Important Questions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Learn Cbse
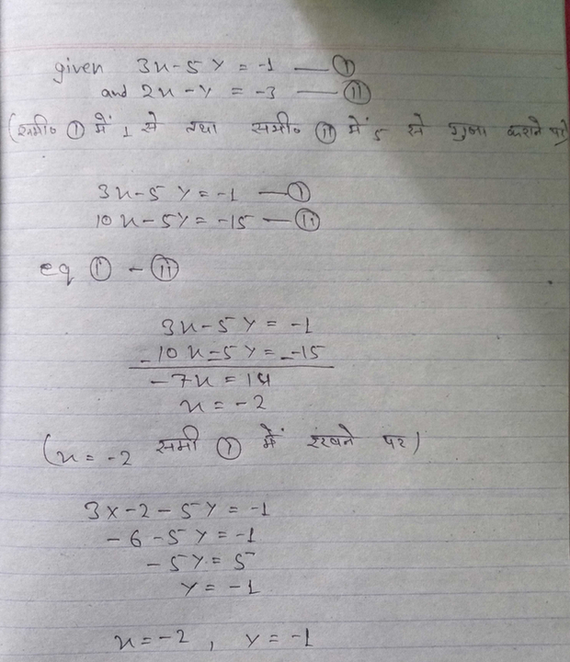



Solve By Substitution Method 3x 5y 1 And 2x Y 3 Scholr



Nanopdf Com




2x Y 3 3x Y 7 Solve This By Elimination Method Maths Algebra Meritnation Com




Omtex Classes 3x Y 2 2x Y 3 Solve The Following Simultaneous Equations Graphically




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 5
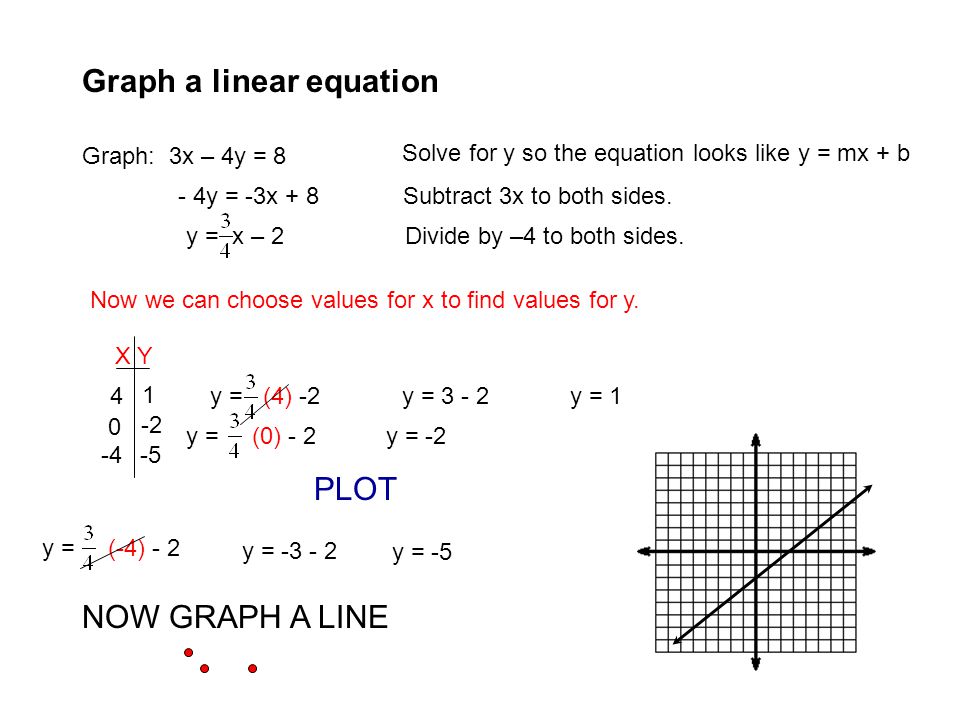



Graph A Linear Equation Graph 2x 3y 12 Solve For Y So The Equation Looks Like Y Mx B 3y 2x 12 Subtract 2x To Both Sides Y X 4 Divide Ppt Download




Ncert Class 10 Mathematics Chapter Wise Questions And Answers And Solutions



Draw The Graphs Of The Equations 2x Y 3 And 3x 2y 1 On The Same Coordinate Axes Also Find The Point Of Intersection Of The Two Lines From The Graphs




Writing Linear Equations From Slope And A Point Bingo Card




3x Y 2 2x Y 3 Practice Set 1 2 Solve Graphically Linear Equations In Two Variables Youtube
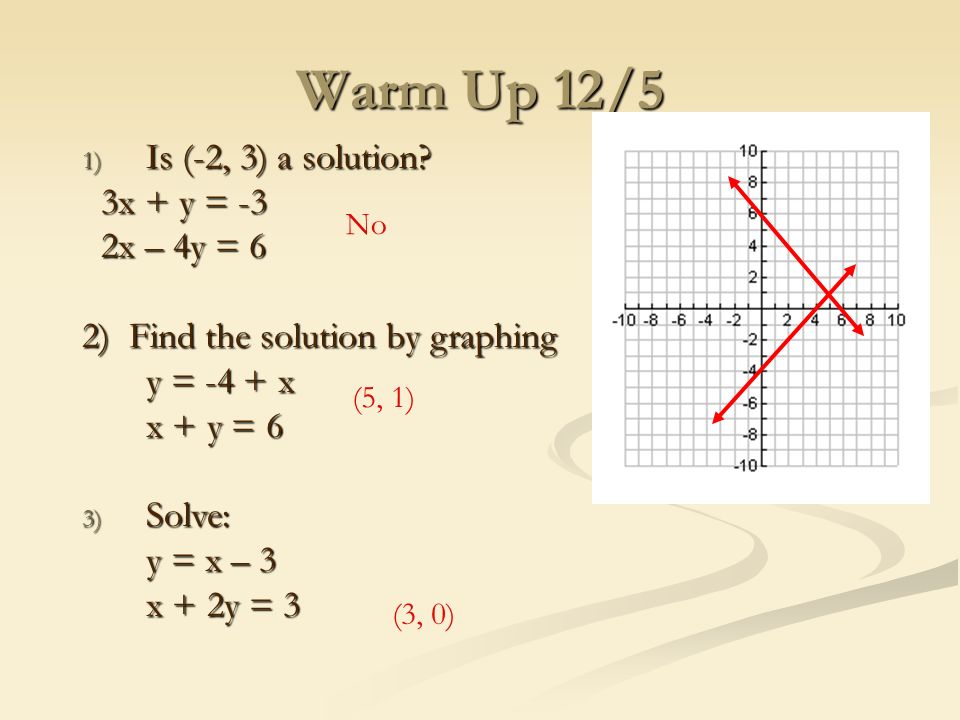



Warm Up 12 5 1 Is 2 3 A Solution 3x Y 3 3x Y 3 2x 4y 6 2x 4y 6 2 Find The Solution By Graphing Y 4 X X Y 6 3 Solve Ppt Download
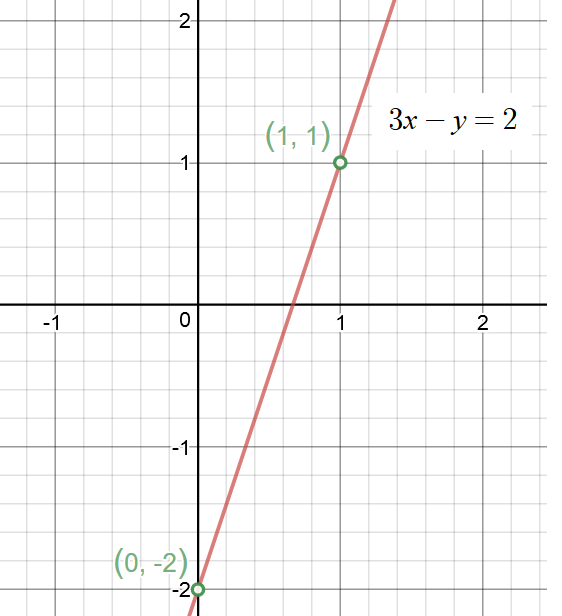



How Do You Graph Using Slope And Intercept Of 3x Y 2 Socratic
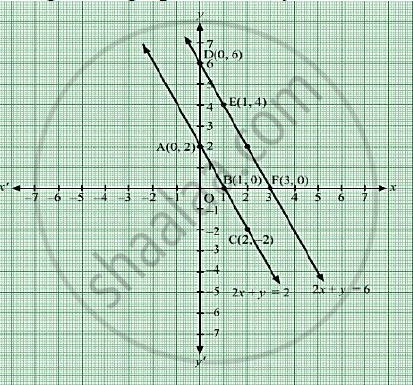



Draw Graphs For Following Equations On The Same Graph Paper 2x Y 2 2x Y 6 Find Co Ordinates Of The Vertices Of Trapezium Formed By These Lines Also



Do The Following Pair Of Linear Equations Have No Solution Justify Your Answer Studyrankersonline
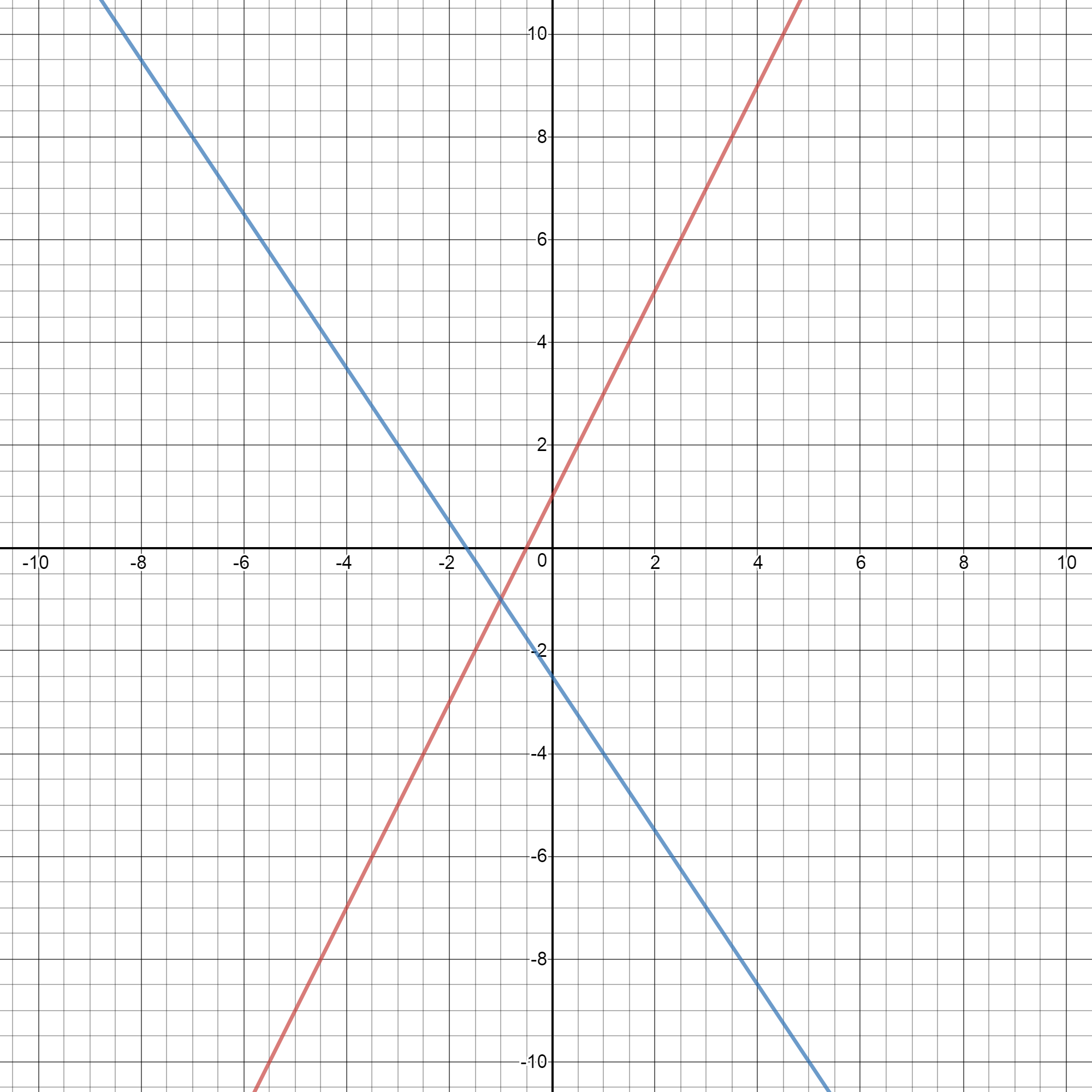



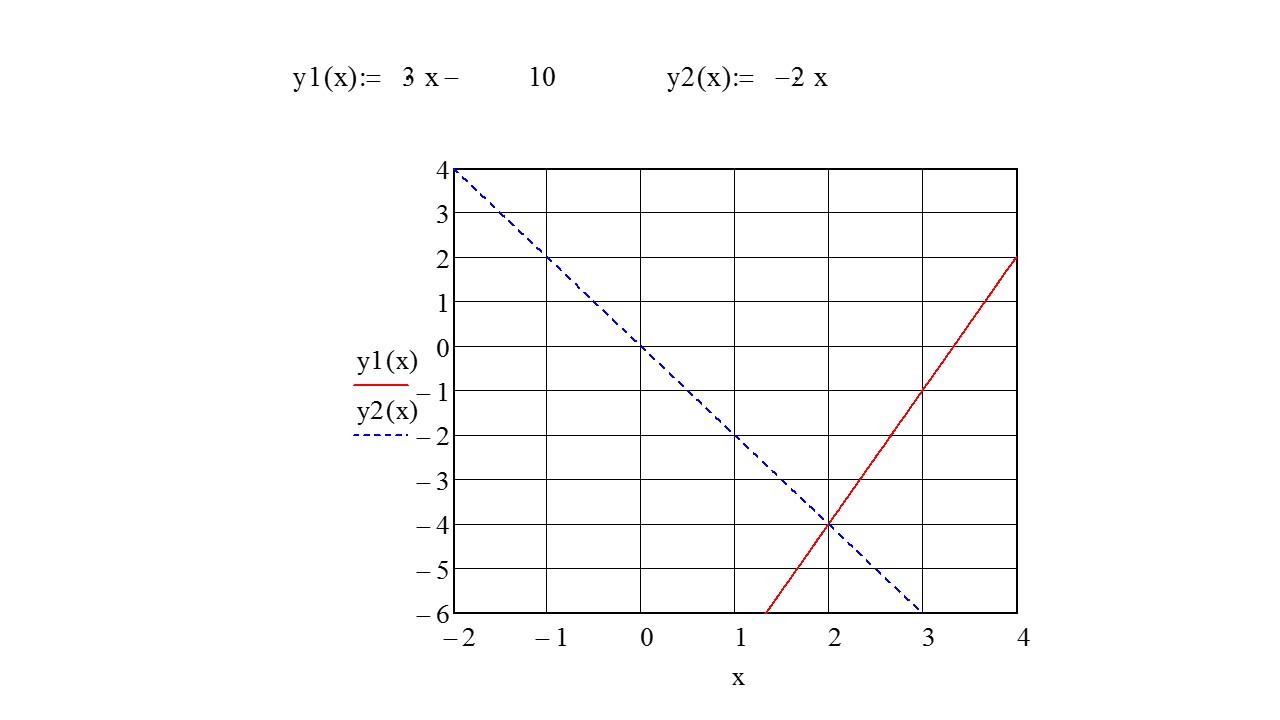
How To Solve The System Of Equations 2x Y 1 And 3x 2y 5 By Graphing Socratic




Solve The Following Simultaneous Equations 2x Y 2 3x Y 7 Brainly In
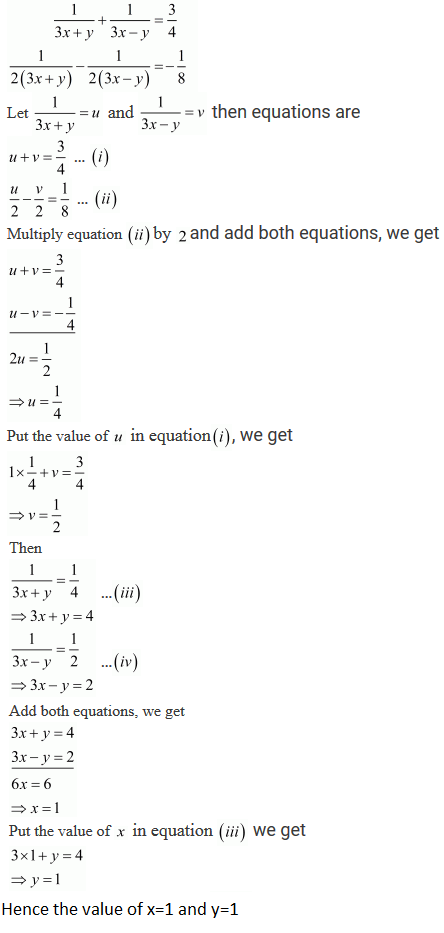



R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Q3d 3x Y 2 0 2x Y 8 Solve The Following Simultaneous Equation Graphically




Solve System Of Linear Equations Using Matrix Method 2x 3y 3z 5 X 2y Z 4 3x Y 2z 3 Mathematics Shaalaa Com
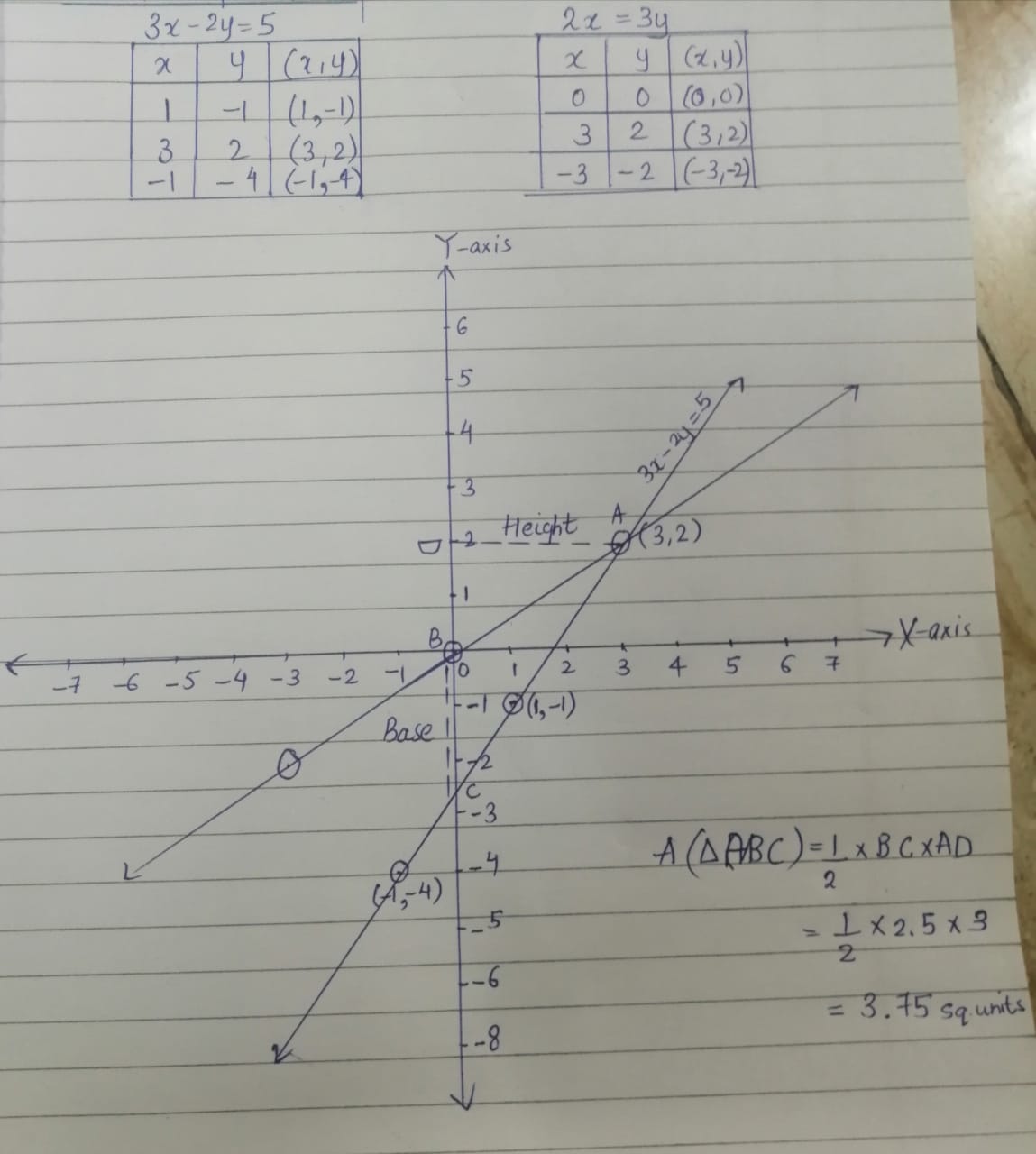



Use Graph Paper For This Question Draw The Graph Of 3x 2y 5 And 2x 3y On The Same Axes Use 2cm 1 Unit On Both The Axes And Plot Only 3



Solve The Following Simultaneous Equations Graphically I 3x Y 2 0 2x Y 8 Ii 3x Y 10 X Y 2 Sarthaks Econnect Largest Online Education Community
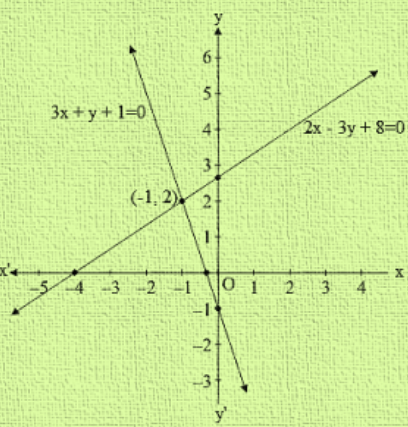



R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2



Solve The Following Simultaneous Equations Graphically I 3x Y 2 2x Y 3 Ii 3x 4y 7 5x 2y 0 Iii 2x 3y 4 3y X 4 Sarthaks Econnect Largest Online Education Community




Misc 9 Find Value Of P 3x Y 2 0 Px 2y 3 0




If The Equation 2x 3y 1 0 3x Y 2 0 And Ax 2y B 0 Are Consistent Then Prove That A B 2 Snapsolve




Solved Activity 2 Find My Value Solve The Following Given Chegg Com



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
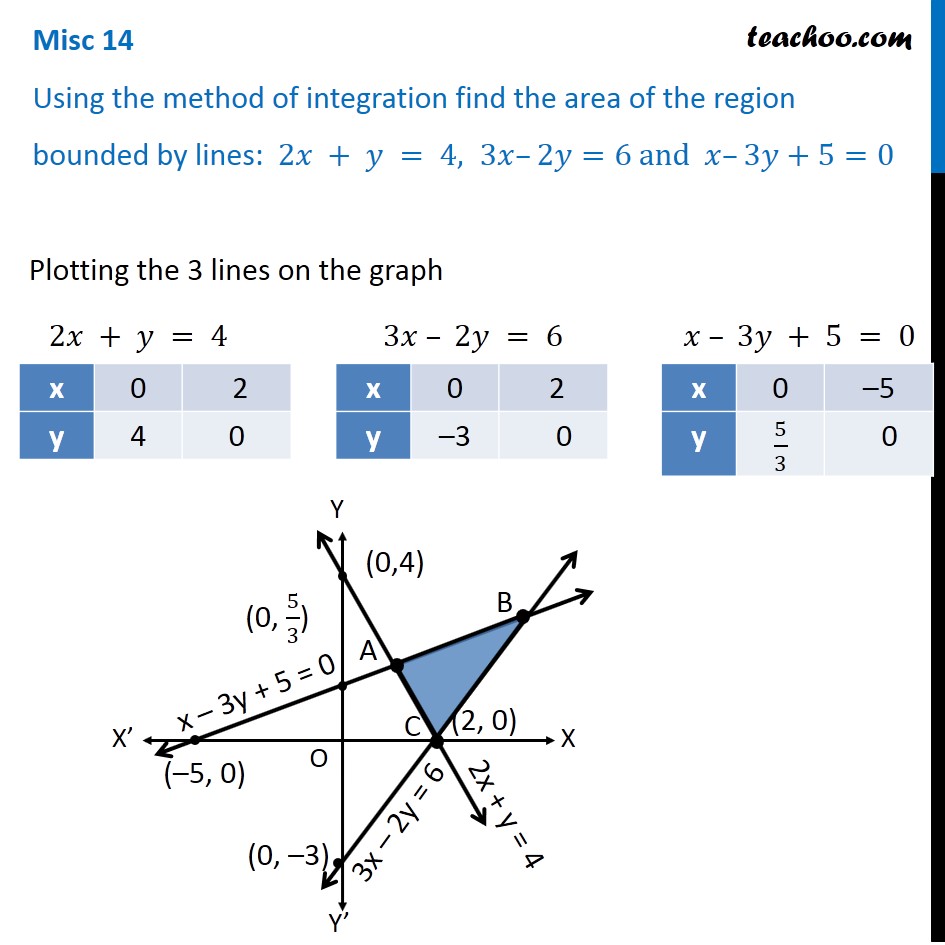



Misc 14 Find Area Bounded By Lines 2x Y 4 3x 2y 6



What Is The Answer For 3x Y 2 Quora



Mathematics 8 Linear Functions



Simultaneous Equations Gmat Math Study Guide




Notes For Systems
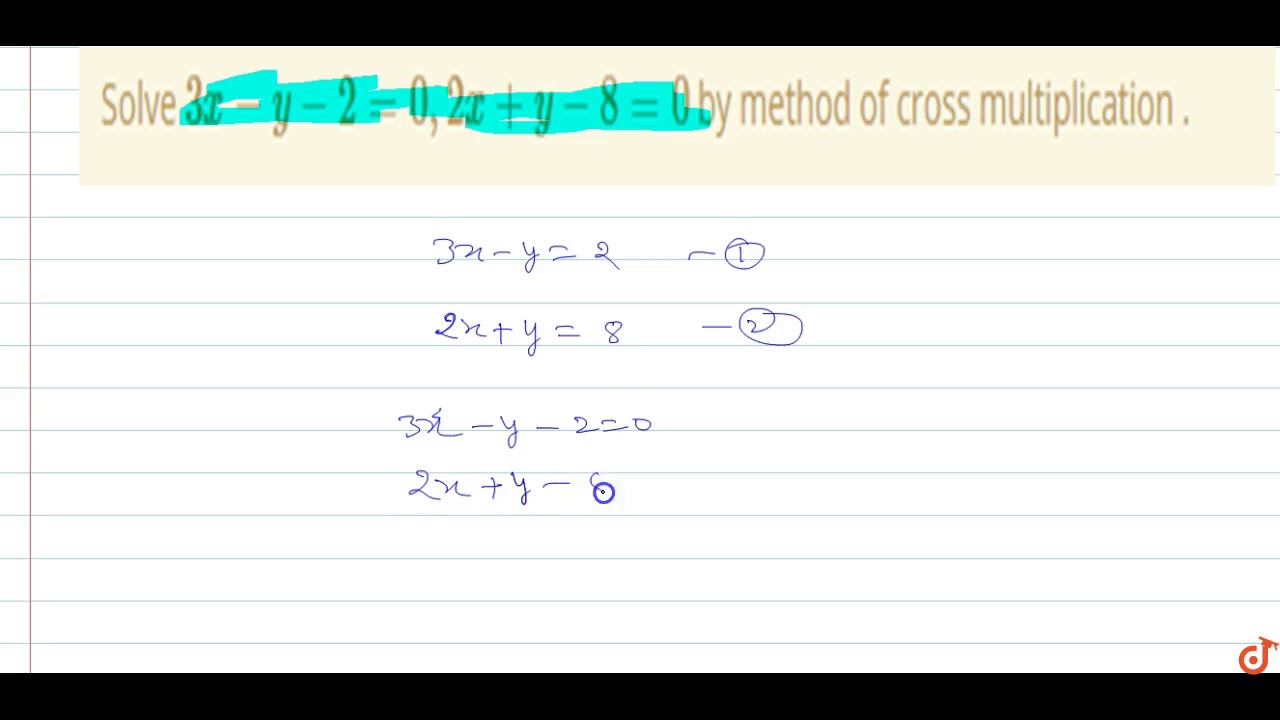



Solve 3x Y 2 0 2x Y 8 0 By Method Of Cross Multiplication Youtube



If 2x 3y 17 And 3x 5y 27 What Are X And Y Quora




Q2 Solve The Following Simultaneous Equations I 2x Y 5 3x Y 5 Ii X 2y 1




Solved 3x Y 1 12 4 O 3 3 5x 4y X 4y 4 4x 3y Chegg Com



3




Solve The Pair Of Linear Equation Of 3x Y 2 0 2x Y 8 0 Brainly In



Graph The Points Using These Two Linear Equations 3x Y 10 And 2x Y 5 Mathskey Com
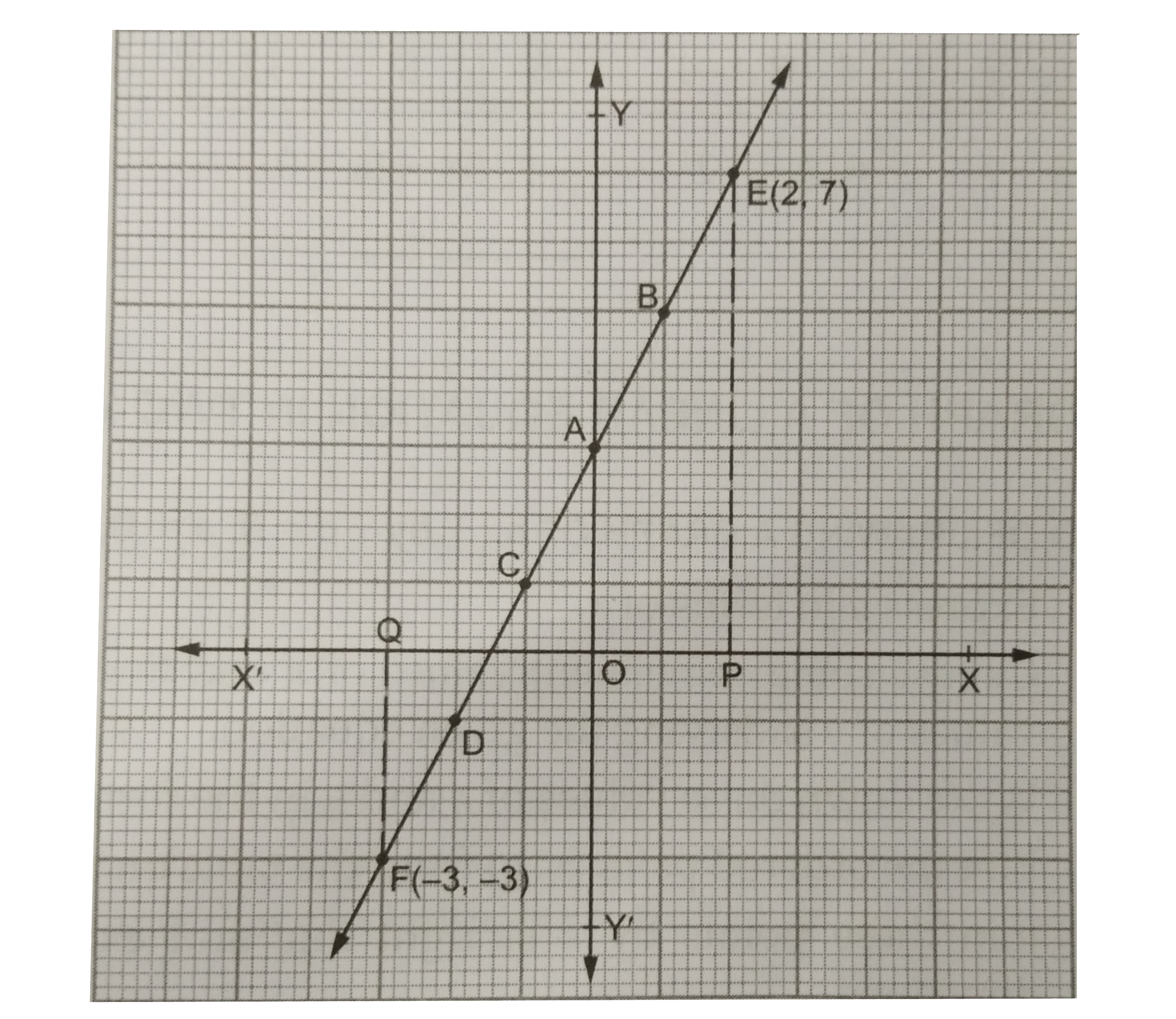



Draw The Graph Of The Equation 2x Y 3 0 Using The Graph Find The Value Of Y When A X 2 B X 3
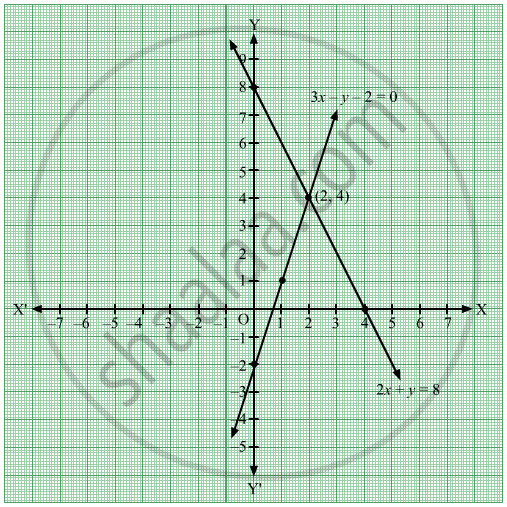



Solve The Following Simultaneous Equation Graphically 3x Y 2 0 2x Y 8 Algebra Shaalaa Com




Solve For Y For Each 1 2x Y 9 2 X Y 2y 4 3x 4 2 Y X 5 7x Y 8 6 3y 1 3x 2x 2x Ppt Video Online Download




Rs Aggarwal Solutions Class 10 Chapter 3 Linear Equations In Two Variables A Plus Topper




If 2x Y 2 5 3x Y 1 3 2 X 2y 1 6 Then



Solution 3x 2y 8 2x 3y 7 Solve Each Of The Following System Of Equations By Graphing



3x 4y 10 And 2x 2y 2




Omtex Classes 3x Y 2 2x Y 3 Solve The Following Simultaneous Equations Graphically




Solved Solve The Following Systems Of Equations By Cramer S Rule 1 X 2y 3 2 2x Y 3 3x Y 1 X Y 6 3 4a 2b 0 Sa




Solved Exercises Use The Substitution Method To Solve Each Chegg Com
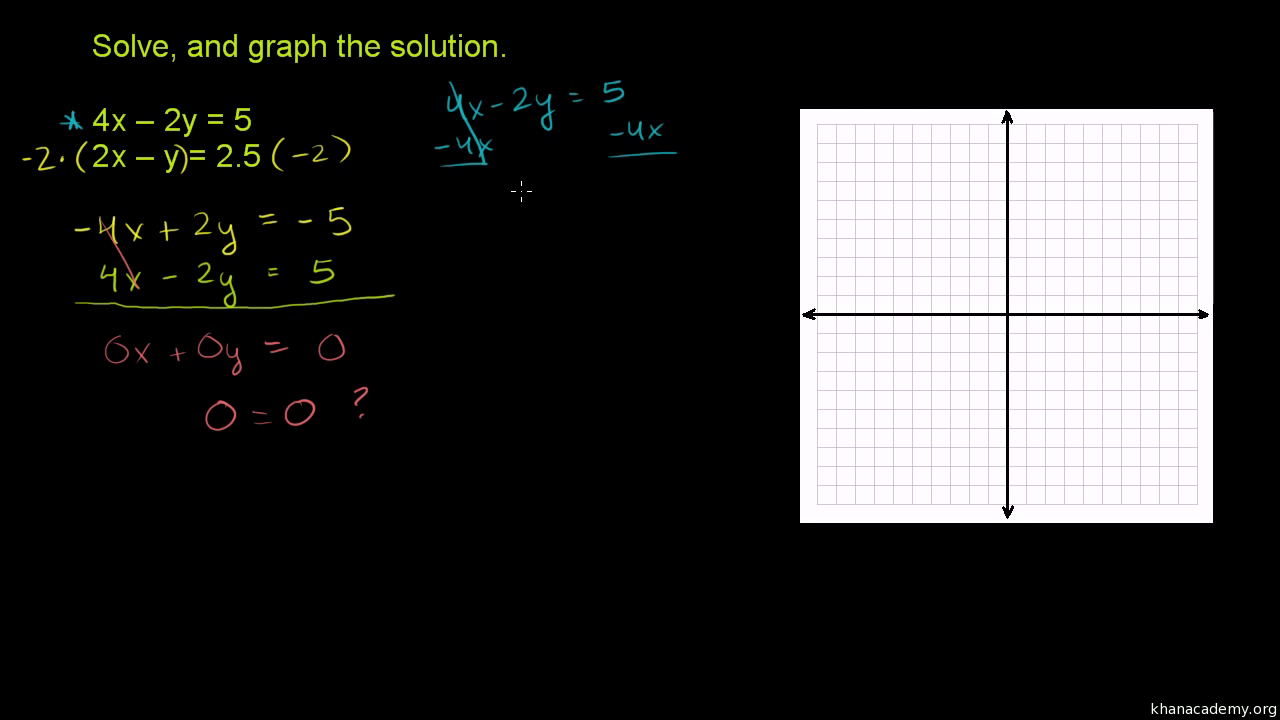



Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy




3x Y 2 2x Y 3 Practice Set 1 2 Graph Simultaneous Equation Graphically Graph Method Ssc Youtube




Exercise 1 2 Cramer S Rule Problem Questions With Answer Solution




Gaussian Elimination To Solve Systems Of Linear Equations
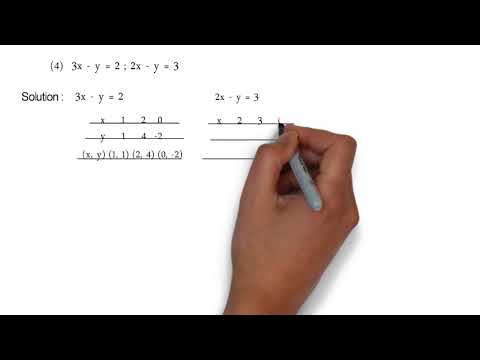



3x Y 2 And 2x Y 3 P S 1 2 Q2 4 Linear Equation In Two Variables Youtube



Moorparkcollege Edu
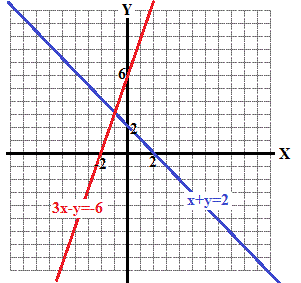



How Do You Solve By Graphing 3x Y 6 And X Y 2 Socratic




Omtex Classes 3x Y 2 2x Y 3 Solve The Following Simultaneous Equations Graphically




Systems Of Equations With Elimination 2x Y 14 6x 3y 42 Video Khan Academy



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora




3x Y 2 2x Y 3 In Graphical Method Brainly In



2x Y 3 Graph


