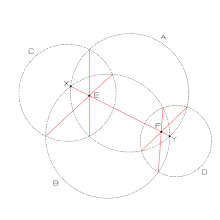
外接円、外心について 「外接円」や「外心」の用語や意味は中学の 教科書の発展内容としてあります。 それぞれの各辺の垂直二等分線は一点でまじわり、その点Dを中心に円を書くと Dを中心に三角形の3つの頂点を通る円を書くことができて、この円 まず、3つの頂点からまでの外心までの距離は外接円の半径であり、全て同じであることに注目しました (下図の赤線は全て同じ長さ)。 すると、各頂点を中心とした3つの円の交点が外心座標であることに気付きます。 つまり、3つの円の方程式が並んだ3連立方程式を解けば外心座標を求められそうです。 { ( p x − a) 2 ( p y − b) 2 = r 2 ( 1) ( p x − c) 2 ( p y − d33 2本の垂直二等分線が交わるところが中心だ! 4 円の中心作図の練習問題に挑戦! 5 円の中心の作図まとめ! 51 Share this 52 関連
円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典
円 中心 求め方 3点
円 中心 求め方 3点-次の図の2点A (a,b),B (c,d)間の距離ABを求めるには,直角三角形を作り,ピタゴラスの定理(三平方の定理)を用いて斜辺を求めます. なお,この公式は,a=cのときやb=dのときでも成り立ちます. 次の2点AB間の距離に等しい値を右の欄から選びなさい. 3点中心(a,b)で半径r、円周の任意の点を(x i,y i)とすると円は以下の式で表せます。 rと中心とx i,y i 間の距離の差を出す式をとりあえず差を0として作成します。 上記の式を二乗すると 左式を使って上式からカッコを取り除きシンプルにします。



コンパスと定規を使った渦巻き線 アルキメデスの螺旋 の描き方 図形の描き方022a 夏貸文庫
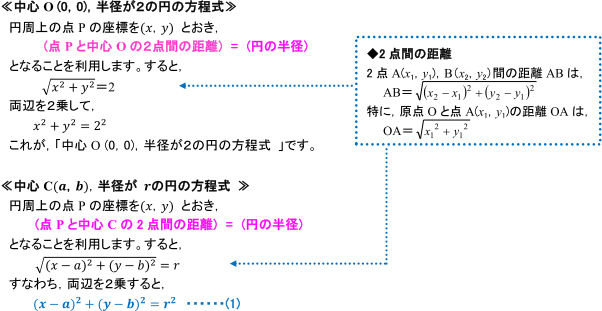
円の方程式とは? 円の方程式とは、 中心の座標と円の半径を用いて、円を方程式で表したもの です。 表し方には「基本形」と「一般形」の \(2\) 通りがあります。 基本形の公式 円の方程式を基本形で表現すると、円の中心と半径が一目でわかります。では,円の方程式の導き方を確認しましょう。 ここでは,『「円周上の点」と「中心」の距離』と『半径』が同じということを利用して,円の方程式を導いてみます。 さらに,この式を展開して整理すると, x 2 y 22ax2bya 2 b 2r 2 =0 となります。3点で円の芯出し・測定をするプログラム 3点の座標から丸物の中心座標と半径を算出するプログラムです。 パソコンに座標を入力する必要がなく、NC設備内で計算を行い、その場で計算結果を出してくれます。 用途に応じて、下記の2種類のプログラムを用意しました。 芯出しバーなどの測定ツールを使用し、各3点の現在位置の機械座標を読み込んで計算を行う
2 垂直二等分線で等しい距離にある点を作図! 3 円の中心の作図方法! 31 円周上に3つ点をとる; 円の方程式の一般形 任せて下さい! 3点を通る円の方程式を求める場合は, x 2 y 2 l x m y n = 0 とおく。 求める円の方程式を x 2 y 2 l x m y n = 0 とおく。 3点 A ( − 2, 6), B ( 1, − 3), C ( 5, − 1) を通るから, { ( − 2) 2 6 2 − 2 l 6 m n = 0 1 2 ( − 3) 2 l − 3 m n = 0 5 2 ( − 1) 2 5 l − m n = 0 これらを整理して, 簡単計算!2つのサイコロの確率の求め方がわかる3ステップ 中3数学 平行線と線分の比の問題の解き方がわかる3ステップ 中3数学 中3数学弦の長さを求める問題の解き方3ステップ
九点円の中心を n n n とおくと, n n n は外心 o o o と垂心 h h h の中点 となります。このことから, n n n もオイラー線上にあることが分かります。 →オイラー線の3通りの証明; 3点を通る円の中心を求める解法はわかりますが、4点以上の多点を通る場合は、どのような求め方があるでしょうか?どなたかわかる方アドバイス願います。#3の続きです。e=(xa)^2(yb)^2r^2を展開して、e = 2ax 2by a^2b^2r^2右図5において,原点を中心とする半径5の円の方程式を求めてみよう. 円周上の点 P の座標を (x , y) とおくと,ピタゴラスの定理(三平方の定理)により, x 2 y 2 =5 2 (A) が成り立つ. 上半円については, y ≧ 0 なので, y= (B)




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典
下図において,線分 CP が点 C を中心に角度θ (180°< θ < 180°) だけ回転した結果, 線分 CQ になったとする.3つの点の座標 C=(Cx, Cy), P=(Px, Py), Q=(Qx, Qy) が与えられたとき,この回転が右回りか左回りかを判別せよ.(別の言い方をすれば,「C → P → Q → C は右回りか左回りか?(a,b)(c,d)(e,f)を通る式x^2y^2lxmyn=0のl,m,nと円の中心点の座標及び半径を求めます 指定した3点を通る円の式 高精度計算サイト ゲストさん求め方 3点を通る円の中心は、その三点を頂点とする三角形の外心となる。 (求める円はその三点を頂点とする三角形の外接円) 三角形の各辺の垂直二等分線の交点がその三角形の外心となる。 外心は3つの頂点から等距離にある。 その外心から各点の




3次元上の3点を通る円の中心を求める ツールあり お助け技術者 陽翔 Note




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4
3母点の接点円の中心の求め方 母点p1、p2及びp2、p3の垂直2等分線をy1=a1x1+c1 y2=a2x2+c2とする それぞれの垂直2等分線の傾きを a1 AB、BCの各垂直二等分線の交点P(X,Y)が円の中心座標、半径はAPとなることから解けます。 解は円の中心(29/3,11),半径=(√3445)/3 がでてきます。 参考URLをご覧下さい。 公式は複雑で覚えるのが大変でしょう。 http//wwwgeocitiescojp/TechnopolisMars/87(1)求めたい2つに"0"を入れる、空白にしない、ということをやられていない (2)あり得ない値を入れられている(例えば弦長のほうが弧長より長いなど) (3)入力するのは2つ、0にするのも2つなのを数が間違っている。 があります。




中1 作図 円の中心を求める方法を解説 数スタ



コンパスと定規を使った渦巻き線 アルキメデスの螺旋 の描き方 図形の描き方022a 夏貸文庫
3点p, q, rで決まる円の 中心をc とするとき, p, q, rはc から最も遠い 点である. このような3点から等距離にあって,しかもそれら3点が その点からの最遠点になっているような点は何通りあるか? これが包含円の個数と同じ. この点と,P1,P2,P3 との距離がどれも (√)/362 であることを確かめてください. また,当然のことながら,この点は3点を通る平面 29x2y45z=67 上にあることが代入すればわかります. 1人 がナイス!以下の入力フォームに3点の座標をを入力し計算ボタンをクリックすると円の方程式を求めます。 x1,y1 x2,y2 x3,y3= ここでは、円の方程式を使用せずに、コンパスと定規で作図する方法に準じて、2辺それぞれの垂直二等分線の交点から円の中心を求めます。




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中点の座標の求め方 中学1年数学 Youtube
球の中心の求め方 前回のコラムで3次元空間での円の中心の求め方について記述したので、次に空間内にある球の中心を求めるロジックについて考えてみます。 球については、表面上にある4点の座標が指定されたら形状が確定します。 (3点の座標と半径 ・任意の3点で円が描画できるw ・円の中心までの距離は同じ(半径)w ・2点間 (a,b) (c,d) の距離を求める計算式・・ L=√((ac)^2(bd)^2) ※二乗=^2 っと言う事で、任意の3点の座標を A(aX,aY) B(bX,bY) C(cX,cY) 円の中心の座標を P(pX,pY) 半径をRとしたとき、3つの点から円の方程式を求める 円の方程式は の他に ① と表すこともできます。 ※円の中心、半径の長さがわかる時に使用 ※3つの点を通ることがわかっている時に使用 このようにして使い分けます。 それでは早速、①を使っ
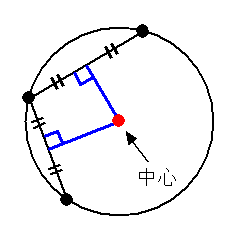



3次元空間での円の中心の求め方 Inak Engineering Llc
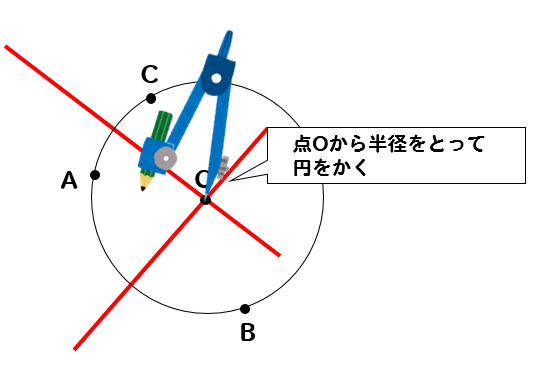



中1 作図 円の中心を求める方法を解説 数スタ
曲率円の例(点pを動かしてみよう) x y 平面で定義された曲線 y = f ( x ) 上の点 P ( x 0 , y 0 ) から曲線に沿って Δ s だけ変位した点を Q とする.この Δ s 部分を円弧とみなし,その円の中心を点 C ,角PCQを Δ α とすると,この円の半径は 円の中心を求める まずは、中心を求めたい円の周上にコンパスの針の部分を置いて、 少し大きめの半円を書くよ 周上の他の場所にも、コンパスの針を置いて さっきと同じ大きさの半円を書くよ そして、半円2つが重なった2点を結ぶ線を引くよ 最後に、もう1つ他の周上にコンパスの針を置いて半円を書くよ また線を書いて、3点を通る円の作図の考え方としては 円の中心を求める⇒中心にコンパスの針を置いて円をかく という手順になります。 それでは、先ほどの問題と同じように 円の中心を求めていきましょう。 3点のうち2組の垂直二等分線をかきます。
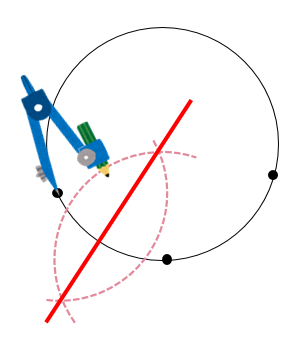



中1 作図 円の中心を求める方法を解説 数スタ



3点から円の中心と半径を求める Satoh
す。面の場合は3か所、円の場合も3か所、球 の場合は4か所の点が必要となります。 図2 要素を定義するのに必要な点 このようにして求められた要素間の位置関係 も、計算によって求めることができます。 図3 2次元(XY)要素の組み合わせ計算例円の方程式の決定(通る3点など) 円と直線の位置関係 円と直線の方程式を連立してできる2次方程式ax bx c2 0 の 判別式D b ac 2 4 に注目すると,次のようになる。 円が直線から切り取る線分の長さと中点 弦の長さの求め方 ①OM AB なので、中心と直線の距離OM を 実は円の方程式を求める問題では、この「3点を通る」という場合が一番計算量が多いです。 円は中心と半径があれば①の方程式 \( (xa)^2(yb)^2=r^2\) にあてはめるだけで良いのですが、3点が与えられる問題では中心も半径もわかりません。




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典
3点 (0,3), (1,0), (3,4)を通る円を考えればよいので、円の方程式を x^2 y^2 lx my n = 0とおき、3点の座標を代入すると 9 3m n = 0 1 l n = 0 25 3l 4m n = 0 これを解いて、 l = 4, m = 4, n = 3 つまり、外接円の方程式は x^2 y^2 4x 4y 3 = 0 (x 2)^2 (y 2)^2 = 5 となり、外心は、 (2,2)です。 7人 がナイス! しています3 円形部分の輪郭の求め方 外接円中心方式,内 接円中心方式および最小領域中心 方式は,い ずれも円形部分の輪郭図形を求めることが必 要である。また,平 均円中心方式でも輪郭に応じた電気 信号を求める必要がある。そこで,つ ぎに円形部分の輪 郭の求め



円の方程式の公式は 3分でわかる意味 求め方 証明 3点を通る円の方程式



2 つの円の位置関係 思考力を鍛える数学




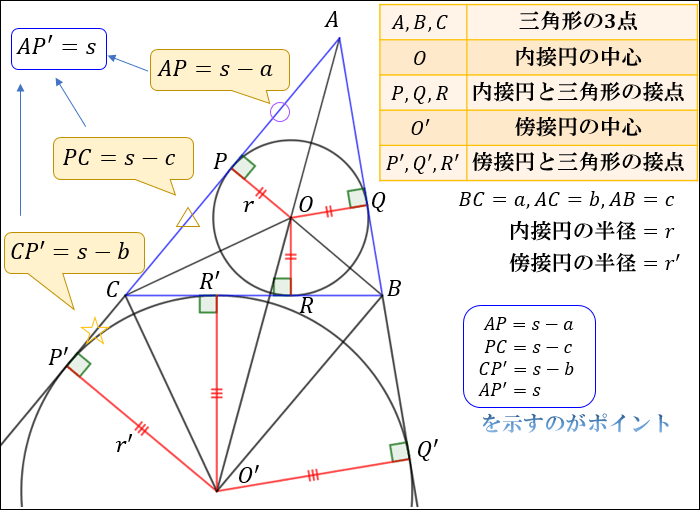
内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ



円の方程式の公式は 3分でわかる意味 求め方 証明 3点を通る円の方程式



円 数学 Wikipedia



円の方程式の導き方 数学 苦手解決q A 進研ゼミ高校講座



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



円の方程式の公式は 3分でわかる意味 求め方 証明 3点を通る円の方程式
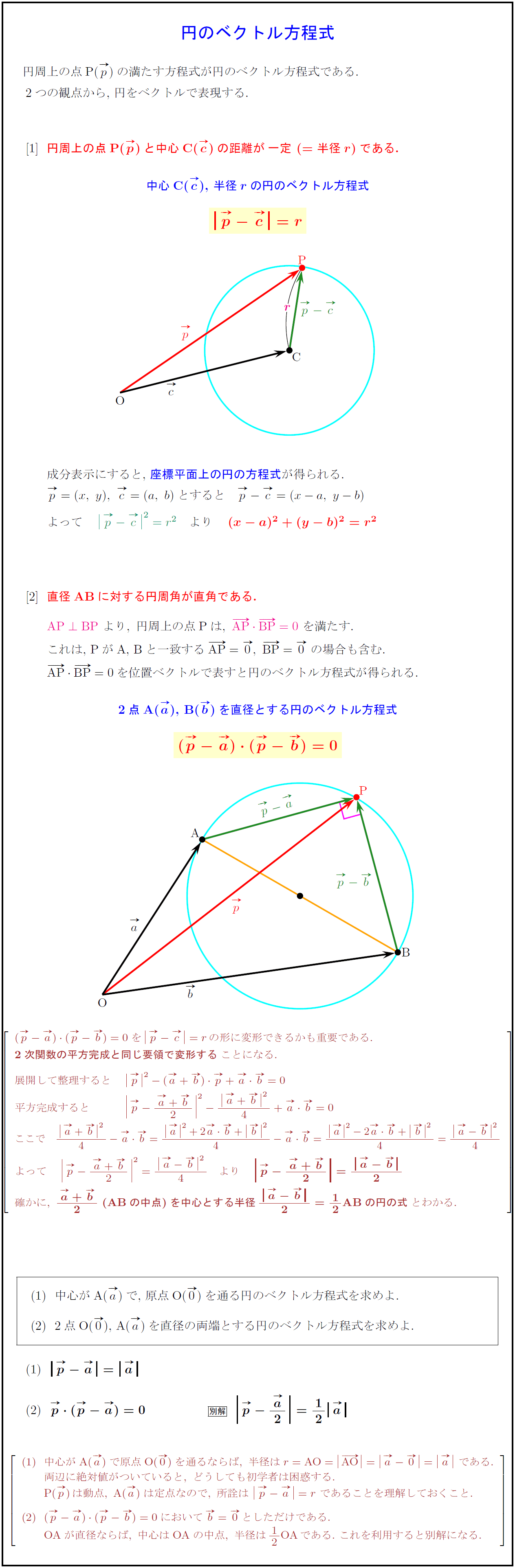



高校数学b 円のベクトル方程式2パターン 受験の月




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
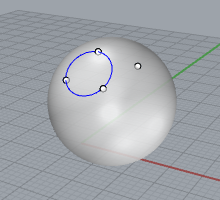



球の中心の求め方 Inak Engineering Llc




作図により円の中心の求める方法について質問です ある円で任意の異 数学 教えて Goo




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



3点を通る円の方程式を求める方法




中学数学 三平方の定理 円錐 のポイントと練習問題




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



Q Tbn And9gcs8govrxmmsri Uq2ku4tuxauhmioafyuowrywnpq8yleyditf9 Usqp Cau




3点を通る円を求める Qiita



外接円 外心について



円周上の3点から円の中心を求める




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
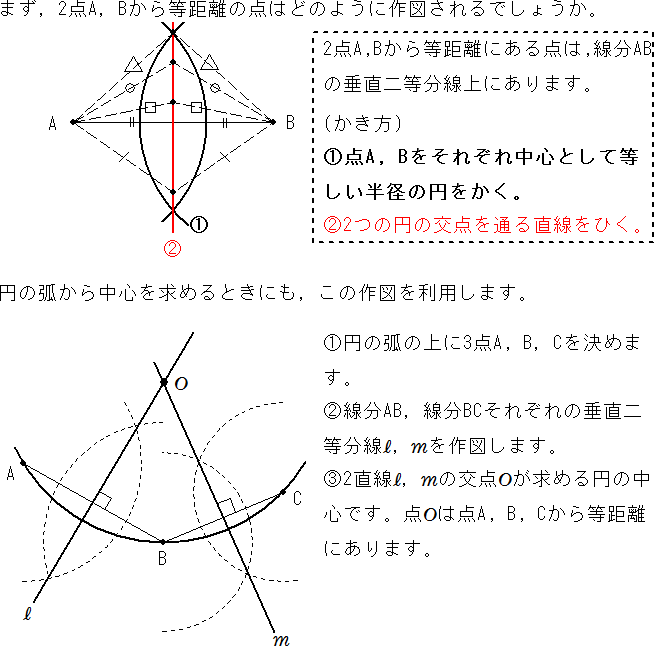



平面図形 円の中心を求める作図 中学数学 定期テスト対策サイト
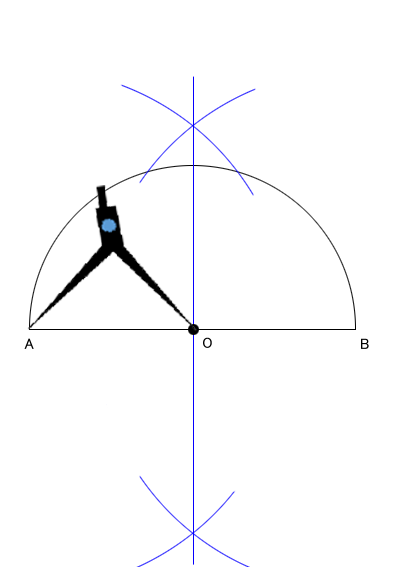



平面図形 おうぎ形 4 ネット塾



中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角形の外心について知っておきたい知識まとめ 理系ラボ




3点を通る円の方程式を簡単に求める方法とは 大学入試数学の考え方と解法




3点を通る円を求める Qiita
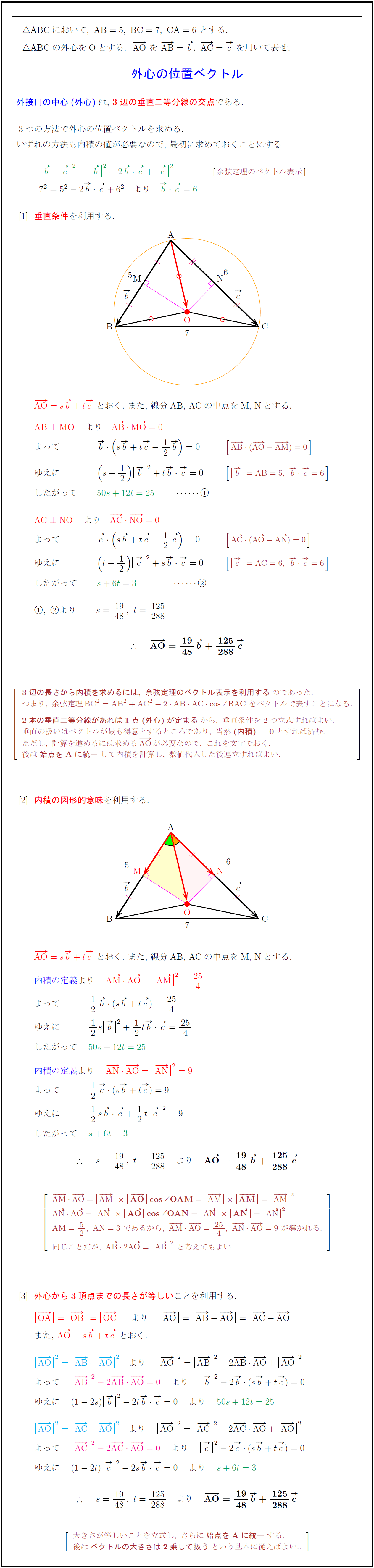



高校数学b 三角形の外心の位置ベクトル 受験の月



幾何計算 2点と半径から円の中心点を求めます Satoh




応用 2つの円の交点を通る円や直線 なかけんの数学ノート



3次元空間での円の中心の求め方 Inak Engineering Llc




高校数学 3点を通る円の方程式の決定 練習編 映像授業のtry It トライイット




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト
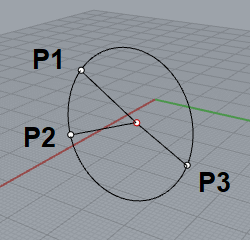



3次元空間での円の中心の求め方 Inak Engineering Llc




2つの点から円の方程式を求める 数学ii By Okボーイ マナペディア



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典
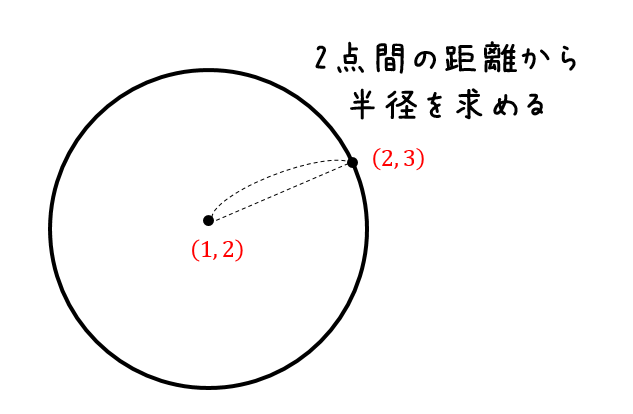



円の方程式の求め方まとめ パターン別に解説するよ 数スタ
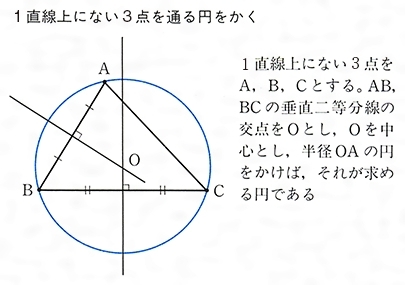



作図とは コトバンク



3



中点と三角形の重心の座標の求め方 思考力を鍛える数学




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




高校数学 三角形の重心公式 映像授業のtry It トライイット




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




3点を通る円を求める Qiita



2つの円の位置関係と共通接線の求め方 図形と方程式 2




中1 作図 円の中心を求める方法を解説 数スタ



円の方程式の公式は 3分でわかる意味 求め方 証明 3点を通る円の方程式




3分でわかる 点と直線の距離の公式の証明 使い方のコツを分かりやすく 合格サプリ



1




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア



二次元図形における円周上の座標 X Y を求める方法を教えてくだ Yahoo 知恵袋




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
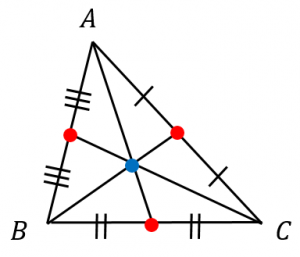



三角形の重心の定義といろいろな求め方 具体例で学ぶ数学



Q Tbn And9gcrctdk8rhp2j 9y R P5bw7yid9pjsk0bzdcawinxs Isywtjrr Usqp Cau




任意の3点を通る円を求める方法 プログラマーのメモ書き




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典




円の方程式の求め方まとめ パターン別に解説するよ 数スタ




円の中心を求める 3つの方法 Wikihow




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典




円 扇形 の面積 周や弧の長さの公式 数学fun
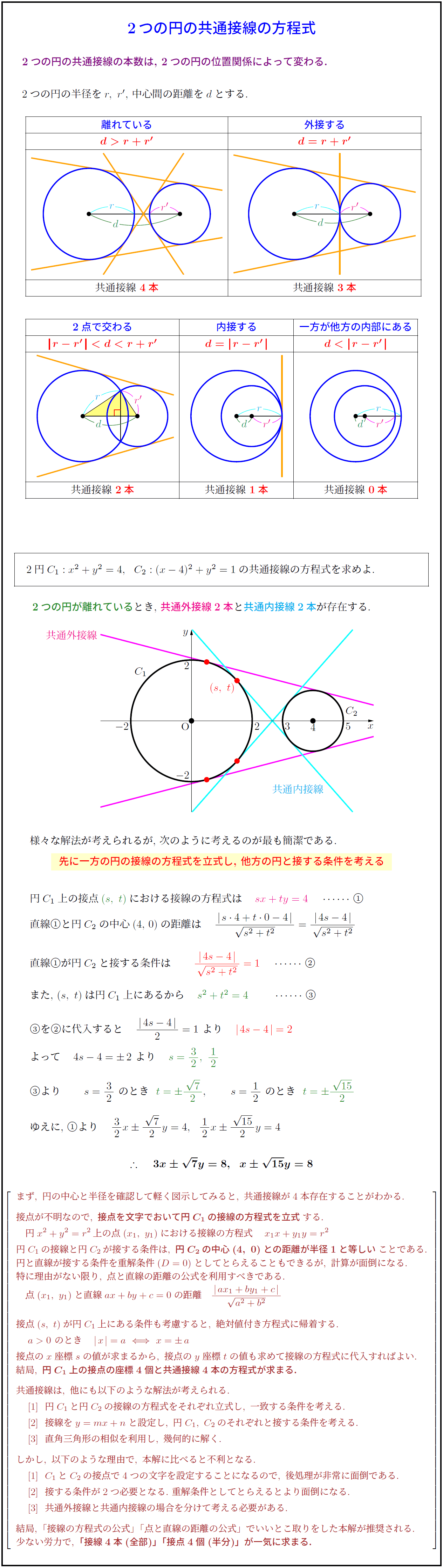



高校数学 2つの円の共通接線の方程式 受験の月



Studydoctorさまざまな円の方程式の求め方 高校数学 Studydoctor
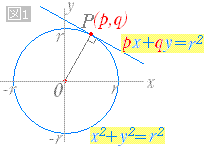



円の接線の方程式
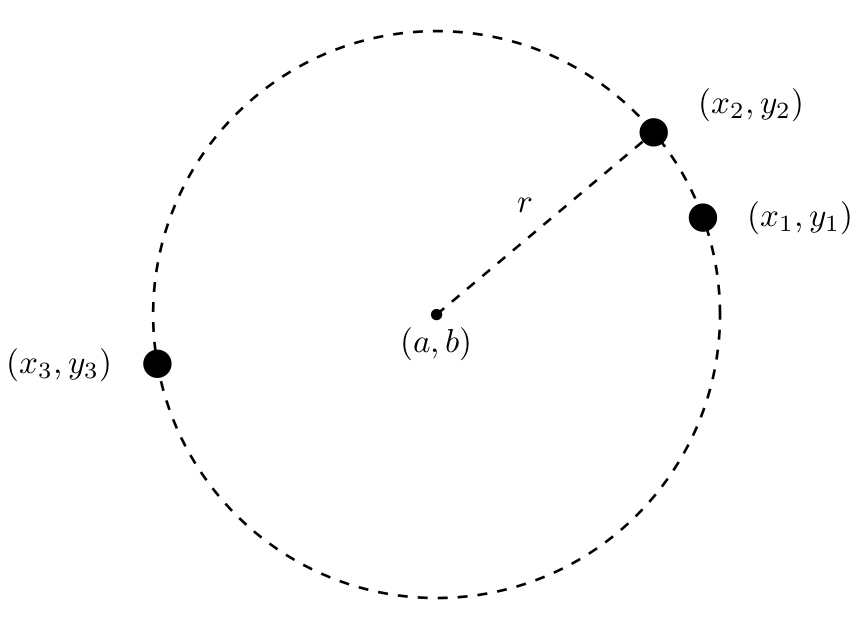



3点を通る円の中心と半径 Notes Jp




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室




円の方程式 数学ii フリー教材開発コミュニティ Ftext
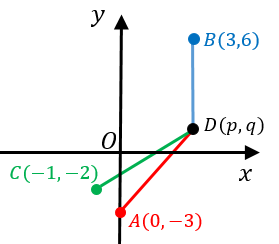



3点を通る円の方程式の2通りの求め方と検算方法 具体例で学ぶ数学




接線の交点 3点を通る円の中心 軌跡 難関大学への数学



中学3年レベル数学座標から円の半径を求める問題について問題集に こんな問題が Yahoo 知恵袋
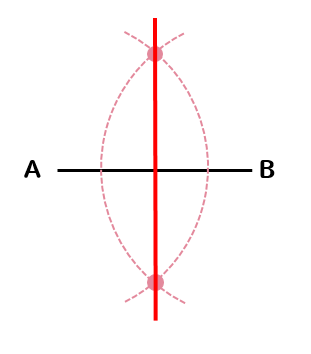



中1 作図 円の中心を求める方法を解説 数スタ




球面の方程式の求め方と問題の解き方をわかりやすく



3点から円の中心と半径を求める Satoh




高校数学 円と直線の位置関係の分類 映像授業のtry It トライイット
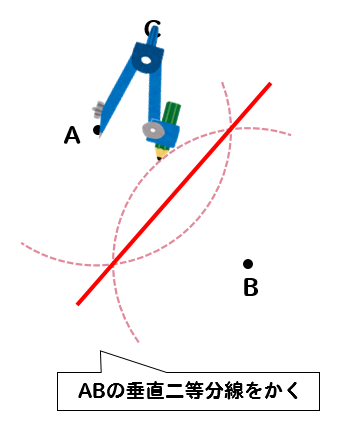



中1 作図 円の中心を求める方法を解説 数スタ




球面の方程式の求め方と問題の解き方をわかりやすく




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
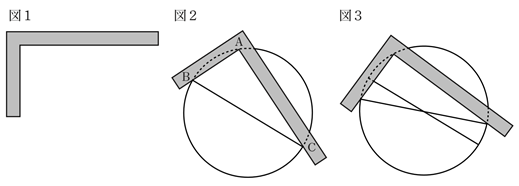



曲尺を使い円の中心を求める 1 準2級 カワズの数学ノート 数学検定 準2級




作図により円の中心の求める方法について質問です ある円で任意の異 数学 教えて Goo




円の方程式 数学ii フリー教材開発コミュニティ Ftext
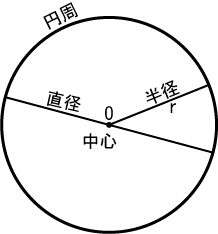



円 数学 Wikipedia




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア
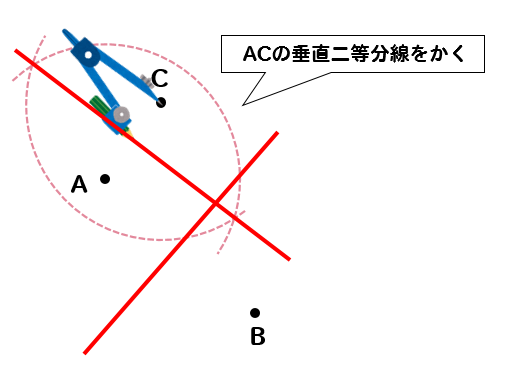



中1 作図 円の中心を求める方法を解説 数スタ
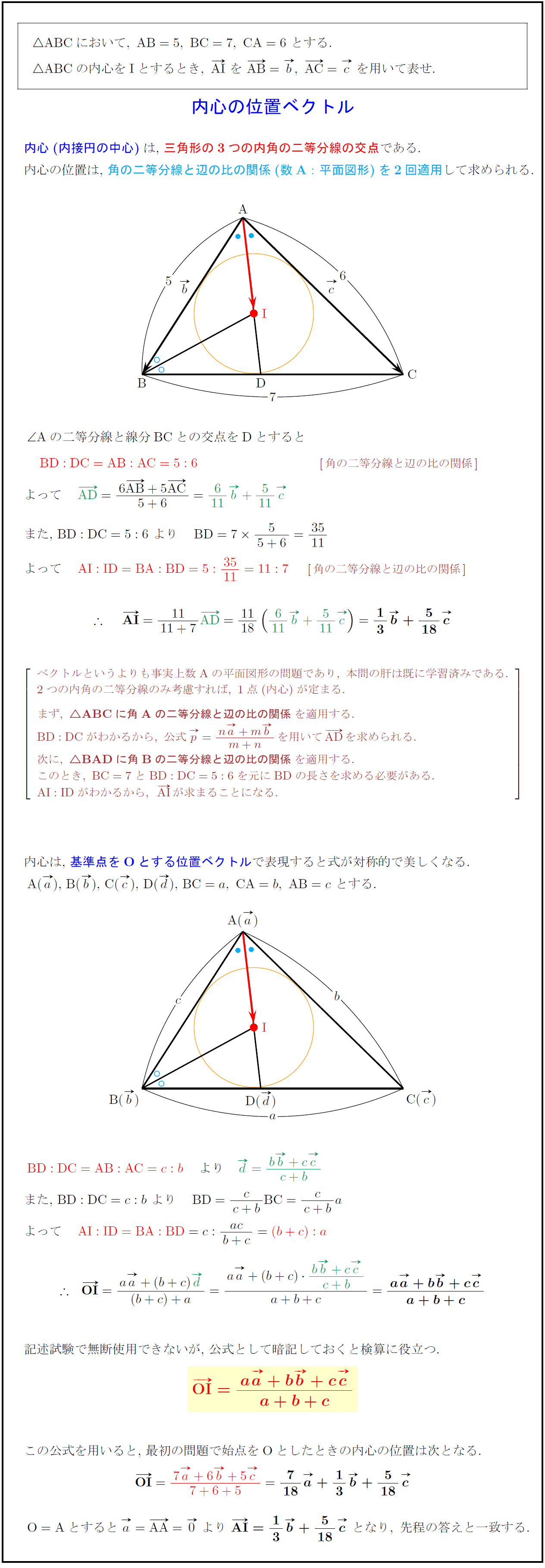



高校数学b 三角形の内心の位置ベクトル 受験の月




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



3点が与えられている三角形の外心の座標の求め方を教えて下さい Yahoo 知恵袋




円の中心を求める 3つの方法 Wikihow




三角形の重心の座標の求め方とその証明 数学ii By ふぇるまー マナペディア


